State Variable Filter Design Equations

State variable filters are useful for filter bi-quads that require a high Q. They are useful as band pass filters. The main draw back is that they require several op-amps in comparison to other topologies such as the Sallen-Key filter. Another useful property is that depending upon where the circuit is tapped as an output, the filter can generate a low pass filter, a high pass filter and a band-pass filter all simultaneously. The figure below demonstrates the various tap points.

We will develop transfer functions for each of the tap points in the circuit. The circuit below represents just one type of state variable filter.

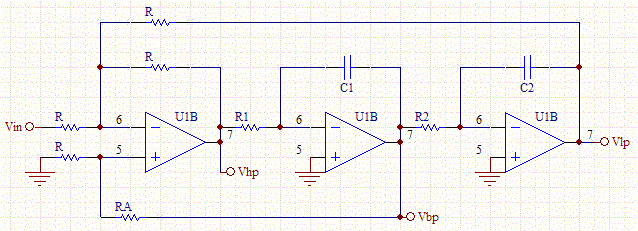
It's easy to show for an inverting configured op-amp:

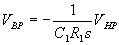
and that

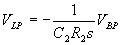
Likewise, using super-position we can show:

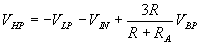
With the above three equations we can derive the transfer function for each of the filter functions. We'll start with the band pass filter:

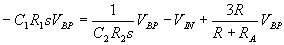
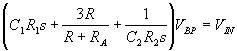
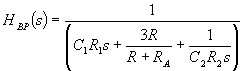
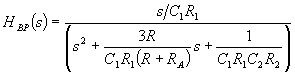
In the same way we can solve for the high pass filter transfer function:

and the low pass filter transfer function:

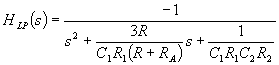
We can now solve for Q and the cut off frequency:

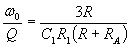
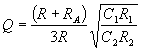
If we let C1=C2=C, then we get the following design equations:

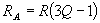
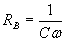
The state variable filter gives us more than enough free parameter, so it is easy to design and tune the Q and the cut off frequency independent of each other.