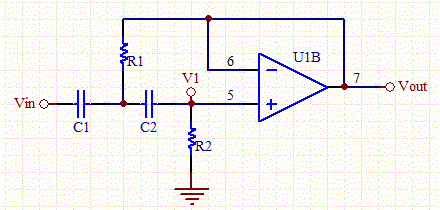
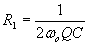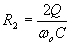Sallen-Key High Pass Filter Design Equations
The Sallen- Key filter is a very popular active filter which can be used to create 2nd order filter stages that can be cascaded together to form larger order filters. The op-amp provides buffering between filter stages, so that each stage can be designed independently of the others. These circuits are suitable for filters which have complex conjugate poles.
When implementing a particular transfer function, a designer will typically find all of the poles, and group them into real poles and complex conjugate pairs. Each of the complex conjugate pole pares are then implemented with a Sallen-Key filter, and the circuits are cascaded together to form the complete filter.
The following link is an easy to use calculator:
The transfer function for a low pass unity gain Sallen-Key filter is:
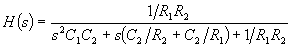
The derivation for this can be found at:
We can transform any low pass active filter to a high pass filter with the following substitutions:
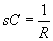
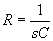
Thus, the transfer function for a unity gain high pass Sallen-Key filter is:
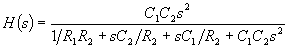
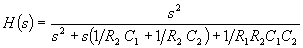
From which we can derive:
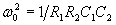
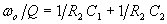
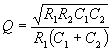
If we set C1=C2=C, then
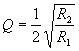
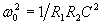
Solving for R1 and R2: